树

# 树：一种分层数据的抽象模型

# 构建方法

利用Object和Array构建树

# 深度/广度优先遍历

深度优先遍历：尽可能深的搜索树的分支。
广度优先：先访问离根节点最近的节点。

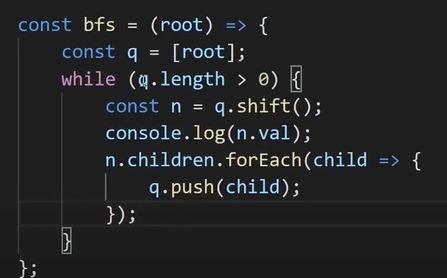
# 二叉树

二叉树树中每个节点最多只能有两个节点，在JS中通常用Object来模拟二叉树。

# 先序遍历

#

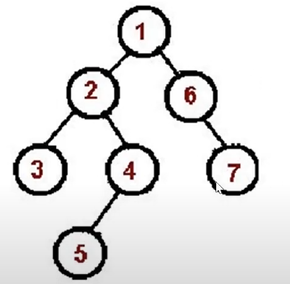
访问根节点
访问根节点的左子树进行先序遍历。
访问根节点的右子树进行先序遍历。

   // 递归版前序遍历
   const preorder = (root) => {
       console.log(root.val);
       prtorder(root.left);
       prtorder(root.right);
   }
   
   // 非递归版
   const preorder = (root) => {
       if(!root) { return; }
       const stack = [root];
       while(stack.length) {
           const n = stack.pop();
           console.log(n.val)
           if(n.right) stack.push(n.right);
           if(n.left) stack.push(n.left);
       }
   }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 中序遍历:左根右

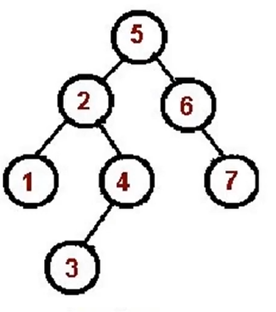
对根节点的左子树进行中序遍历。
访问根节点。
对根节点的右子树进行中序遍历。

// 递归版中序遍历
const inorder = root => {
    if(!root) return;
    inorder(root.left);
    console.log(rooot.val);
    inorder(root.right);
}

// 非递归版
const inorder = (root) => {
    if(!root) return;
    const stack = [];
    let p = root;
    while(stack.length || p) {
        while(p) {
            stack.push(p);
            p = p.left
        }
        const n = stack.pop();
        console.log(n.val);
        p = n.right
     }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 后续遍历：左右根

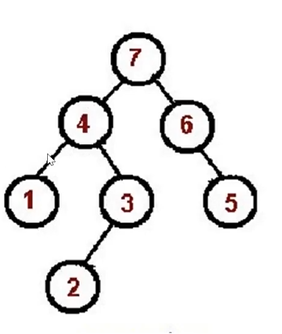
// 递归版本
const postorder = (root) => {
    if(!root) return;
    postorder(root.left);
    postorder(root.right);
    console.log(root.val);
}


// 非递归版
const postorder = (root) => {
    if(!root) return;
    const outputStack = [];
    const stack = [root];
    while(stack.length) {
        const n = stack.pop();
        outputStack.push(n);
        if(n.left) stack.push(n.left);
        if(n.right) stack.push(n.right);
    }
    while(outputStack.length) {
        const n = outputStack.pop();
        console.log(n.val);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 案例

二叉树的最大深度 (opens new window)
1. 记录一个变量记录最大深度
2. 利用深度遍历算法遍历二叉树。
3. 深度优先遍历的过程中记录层级。
4. 遍历过程中遇到孩子节点层数加一
5. 刷新层级，对比最大深度和当前层级。
二叉树的最小深度 (opens new window)
1. 考虑使用广度优先遍历
2. 过程中遇到叶子节点停止遍历，返回节点层级。
二叉树的层序遍历 (opens new window)
1. 使用广度优先遍历；
2. 遍历时需要记录当前节点所处的层级，方便将其添加到不同的数组中，
二叉树的中序遍历 (opens new window)
LeetCode：112 路径总和 (opens new window)
1. 深度优先遍历
2. 遍历过程中记录当前路径的节点值的和。

遍历JSON的所有节点值

const json = { a: { b: { c: 1 } } };
const dfs = (n, path) => {
 console.log(n, path);
 Object.keys(n).forEach(k => {
  dfs(n[k], path.concat(k))
 })
}

1
2
3
4
5
6
7

渲染Antd的树组件：深度优先遍历

# 🔚总结

树是一种分层数据的抽象模型；

树的常用操作；

编辑

上次更新: 2022/02/21, 05:57:00

← 字典图→

树